A vertex-regular polyhedron is one in which, given two vertices 'a' and 'b', there is a symmetry of the model taking 'a' to 'b'. That is, roughly, the polyhedron is vertex-regular if every vertex looks the same as every other vertex. A soccer ball is vertex regular because every vertex is surrounded by two hexagons and one pentagon, so that any vertex can be sent to any other by a symmetry.

Below are examples of vertex-regular models with (full) icosahedral symmetry. (I always mean full icosahedral unless I specify only the rotational part.) A "generic" such model has 120 vertices, corresponding to the 120 elements in the group. The faces in such a model are decagons, hexagons, and rectangles. This means that there are three different types of edges, ones between a decagon and a hexagon, ones between a hexagon and a rectangle, and ones between a rectangle and a decagon. In a typical model, these three types of edges will have three different lengths--clearly, the three different types of edges cannot be mapped into one another by a symmetry of the model, so there is no reason they have to be the same length. If the edges are not all the same length, then the decagons and hexagons will not be regular. Rather, the decagons will have the same *angles* as a regular decagon, but two different, alternating edge lengths, and similarly for the hexagons.

These three types of edges can have any three lengths you like. The edges will always be blue lines, but you can use any three lengths of blue (or half-blue) you like. I have illustrated the point by using small, medium, and long blues. If you make all three types of edges the same length (and nothing prevents you from doing this if you want to), you get the Archimedean solid known as [I don't know the name offhand].

Click on the image to launch vZome with this model.

If you like, you can even shrink one of the three types of edges down to length zero. If you do this, the two vertices at the ends of each such edge get combined, and you get a model with 60 vertices and icosahedral symmetry.

Suppose, for example, you shrink to zero the edges between the decagons and hexagons. Then half of the decagon edges disappear, so the decagons become pentagons. Similarly, half of the hexagon edges disappear, so the hexagons become triangles. The rectangles, meanwhile are left the way they were. We end up, then, with a model having pentagons, triangles, and rectangles as its faces. Such a model will be similar in shape to the Zome connector, except that the two remaining types of edges (between rectangle and pentagon and between rectangle and triangle) can be any two lengths you like. If you make the triangle-rectangle edges one golden ratio longer than the pentagon-rectangle edges, you get precisely the Zome connector. If you make the two types of edges the same length, you get an Archimedean solid known as [..]. Here is a model which is a "stretched" version of the Zome connectors, with the triangles made of long blues and the pentagons of short blues.

Click on the image to launch vZome with this model.

Meanwhile, suppose you shrink to zero the edges between the decagons and the rectangles. Then two opposite edges of the rectangle have length zero, so the rectangle has shrunk to a line segment. Meanwhile, the decagons become pentagons and the hexagons stay as they were. We are left, then, with pentagons and hexagons. Such a model is similar to the soccer ball, except that the edges between a hexagon and a pentagon do not have to be the same length as the edges between two hexagons. If you do make the two kinds of edges the same length, you get a true soccer ball, also known as a buckyball or (the Archimedean version) of a truncated icosahedron.

Click on the image to launch vZome with this model.

Finally, we can shrink to zero the edges in the 120-vertex model between a rectangle and a hexagon. The result is a model with decagons and triangles, but again two not-necessarily equal edge lengths. If you make the edge lengths equal, you get the Archimedean version of the truncated dodecahedron.

Click on the image to launch vZome with this model.

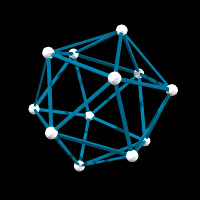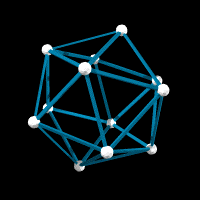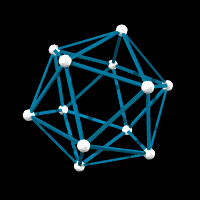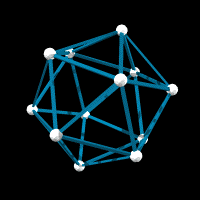
If shrinking one type of edge of the 120-vertex model to zero isn't enough for you, you can shrink to zero two of the three types. Depending on which two you shrink, you get either an icosahedron, a dodecahedron, or an icosadodecahedron.

Click on the image to launch vZome with this model.

Click on the image to launch vZome with this model.

Click on the image to launch vZome with this model.

If you count, there are seven types of vertex regular models with icosahedral symmetry, the "generic" one with 120 vertices, three different types with 60 vertices, and the dodecahedron, icosahedron, and dodeca-icosahedron. I attach models labeled by the number of vertices--NOT the number of faces. The small ones you already presumably have models of, but I include them for completeness.